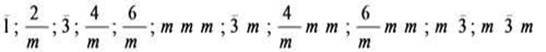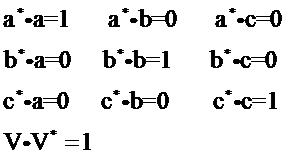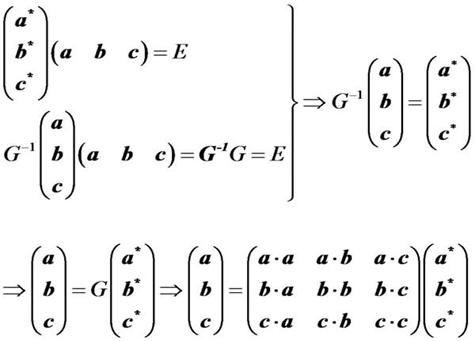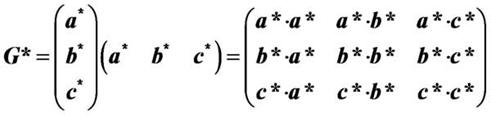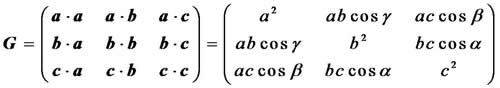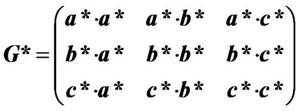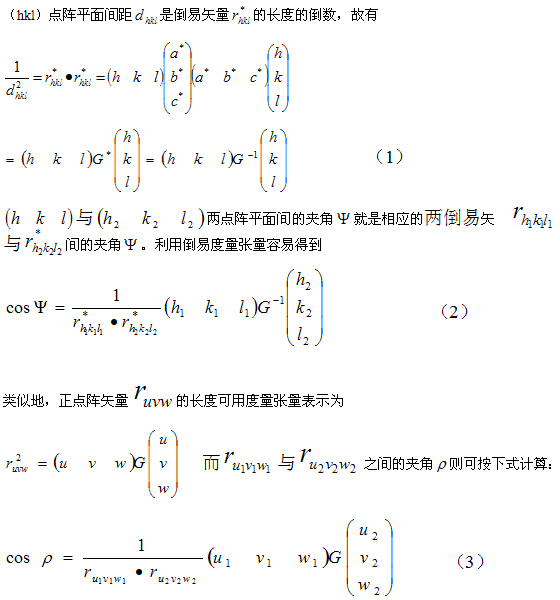第一节 晶体和点阵的定义

1.1 晶体及其基本性质

晶体的定义

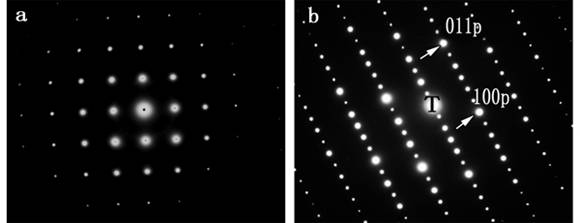
下图为晶体的电子衍射花样，其中图a为一般晶体的电子衍射花样，而图b则是一种具有沿[111]p方向具有六倍周期的有序钙钛矿的电子衍射花样，由这些衍射花样可以看出来，无论是无序还是有序晶体，其倒空间都具有平移周期对称的特点（相应的正空间也应该具有平移对称的特点）。事实上在准晶发现以前，平移周期对称被当作晶体在正空间中的一个本质的特点，晶体学中的点群和空间群就是以晶体的平移对称为基础推导出来的。

晶体的分类

从成健角度来看，晶体可以分成：


面角守衡定律：（由丹麦的斯丹诺于1669年提出）

在相同的热力学条件下，同一物质的各晶体之间比较，相应晶面的大小、形状和个数可以不同，但相应晶面间的夹角不变，一组特定的夹角构成这种物质所有晶体的共同特征。


下图是自然界存在的具有规则外形的几种常见的晶体，分别是方解石、萤石、食盐和石英，它们的面角关系完全符合面角守衡定律。事实上，自然界中的晶体，当其形成条件比较接近平衡条件时，它们往往倾向于长成与其晶体对称性相应的外形。

非晶体的定义

非晶体是指组成物质的分子（或原子、离子）不呈空间有规则周期性排列的固体。它没有一定规则的外形，如玻璃、松香、石蜡等。它的物理性质在各个方向上是相同的，叫“各向同性”。它没有固定的熔点。所以有人把非晶体叫做“过冷液体”或“流动性很小的液体”。

准晶的定义

准晶是准周期晶体的简称，它是一种无平移周期性但有位置序的晶体；也有人将其定义为具有非公度周期平移对称的晶体。准晶可以具有一般晶体禁止出现的五次、八次、十次和十二次旋转对称，但非公度周期平移对称才是其本质特点。下图中为准晶的电子衍射花样和三维准晶的外形，其中图a是二维Al-Ni-Co十次准晶的电子衍射花样，图b是三维准晶沿5次对称轴得到的电子衍射花样，图c为三维准晶的外形。从电子衍射花样可以清楚地看到准晶的非周期平移对称特点。衍射花样中，衍射斑点之间虽然不满足平移对称，但它们之间满足数学上的菲博纳奇数列。



晶体的基本性质　

1）自范性或自限性

就热力学可能性而言，任何晶态的物质总是倾向于以凸多面体的形式存在，晶体的这一性质称为自限性或自范性。

2）具有特定的熔点；

3）晶体的宏观均匀性：均匀性是晶体中坐标原点的任何平移后性质的不变性；

4）晶体的各向异性：晶体的物理性质随方向不同而有所差异的特性，称为晶体的各向异性。

1.2 点阵的定义：

点阵是在空间任何方向上均为周期排布的无限个全同点的集合。

与点阵有关的历史

第二节 晶体中的对称元素与晶体学点群

1.1 晶体中的对称元素

1）对称轴
若形体绕轴转过360°/n（n为整数）后即回复为自身，则该形体具有n次旋转对称，这个轴就称之为n次旋转对称轴。n次旋转对称本身构成一个群。在晶体中，由于受平移对称的制约，只能存在1，2，3，4，6次旋转对称操作。


2）反映面
若形体中的一个面将形体分成两部分，且两部分上的点相对于该平面成镜面对称，则该平面称为该形体的反映面，以符号m表示。反映也构成群。


3）反演中心
若形体中的所有点都相对于某一点中心对称，则该点就是反演中心，用符号-1表示。


4）平移
在晶体中，沿某个周期方向平移一个或多个周期后，我们认为晶体没有发生改变，称之为平移对称。


5）旋转反演
旋转和反演的复合操作构成一个不同于旋转和反演的对称群。


6）螺旋
旋转与平行平移的组合。


7）滑移
反映与平行平移的组合。



1.2 晶体学点群：


将以上点对称操作任意组合，能够构成群的组合有32种，这就是晶体中能够存在的点对称操作组合，称之为晶体学点群。所以晶体中能够存在的点群是32种。

旋转点群：


中心对称的点群：


非中心对称的点群：




第三节 空间点阵


3.1 空间点阵的类型

在讨论点群的时候，讲的是平移对点群对称元素的制约；当晶体中的对称元素确定以后，又会反过来制约平移群和点阵的类型！

无论晶体的点群是否具有中心对称性，当从晶体中抽象出晶体的点阵以后，其空间点阵总是中心对称的！

这是因为晶体中的原子团可以不是中心对称的，但是当将其抽象为空间点阵点以后，阵点总是中心对称的，再加上平移群也显示中心对称的特点，使得空间点阵一定是中心对称的。

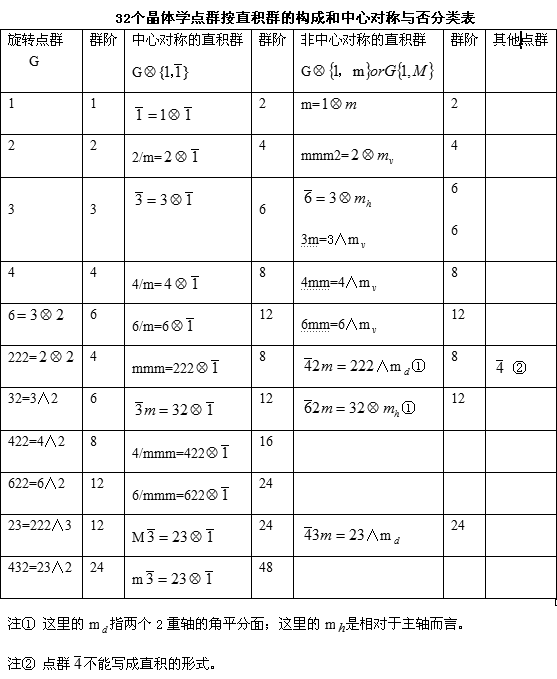
下表是32种点群按直积群的构成和中心对称与否的分类表：






3.2 按点群的对称性分类

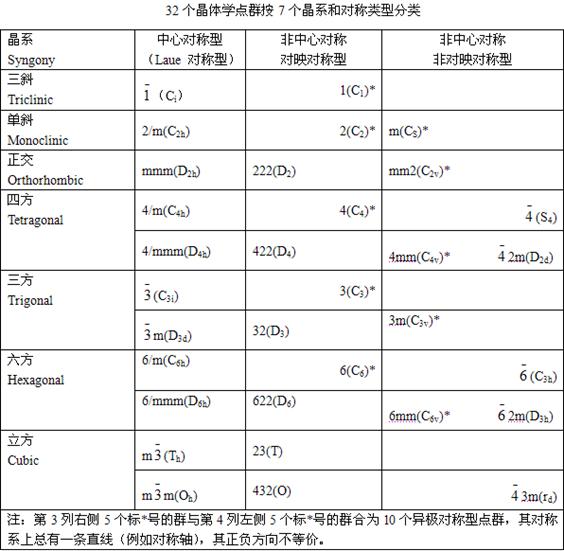
因此按点群的对称性来划分空间点阵时，只须要考虑11个中心对称的点群；另外，这11个中心对称的点群与平移群结合时，将会使其中的4个与另外4个具有完全相同的对称元素；因此只能划分出七个晶系。分别是：
三斜；单斜；正交；四方；三角；六角；立方。（如上表和下表所示）


3.3 按点阵的对称性分类

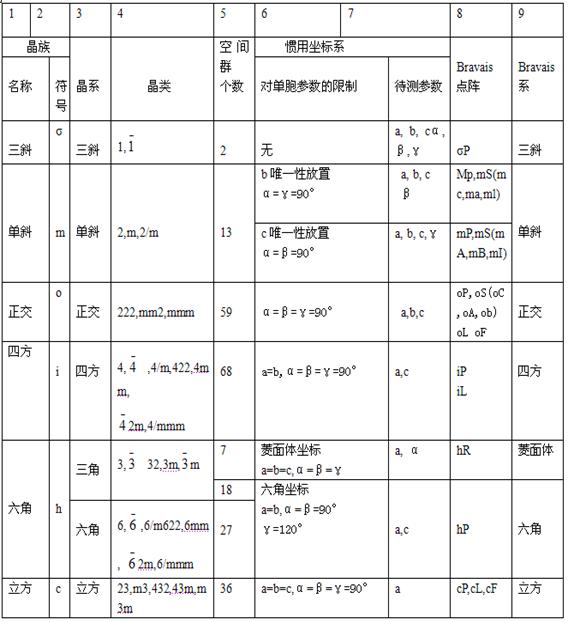
三维空间点阵有6个参数（a，b，c，α,β,γ），在每一组参数下，按照对称性由低到高的顺序，依次考虑点阵的各种点群对称性，一旦不能容纳某些点群时，则变动点阵参数。这样可以得出七种不同的晶体类型，由此可以得到七大Bravais系，分别为：
三斜；单斜；正交；四方；菱面体；六角；立方。（如下表所示）

七大晶系的分类

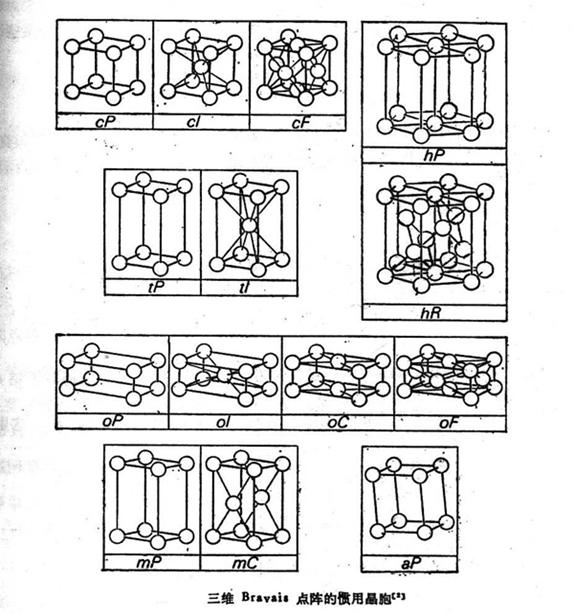
当选用能充分反映点群对称性的惯用晶胞时，可以得到14种bravais点阵，分别是简单立方（cP)、体心立方(cI)、面心立方(cF)、简单四方(tP)、体心四方(tI）、简单正交(oP)、体心正交(oI）、面心正交(oF)、侧心正交(oA,oB或者oC）、简单单斜(mP)、侧心单斜(mA,mB或者mC）、简单三斜(aP)、简单六方(hP)、菱面体六方(hR)。如下图所示：


第四节 倒易点阵及其在晶体几何中的应用

4.1 倒易点阵

倒易点阵的定义：



由倒易点阵基矢的定义，容易推出：




研究倒易点阵的意义：

利用倒易点阵可以比较方便地导出晶体几何学中的各种重要关系式；
用倒易点阵可以方便而形象地表示晶体的衍射几何学；
在物理学中可以用倒易点阵来表示波矢。

倒易点阵的特点：

同名的正倒空间基矢之间点乘等于1，异名的正倒空间基矢点乘的结果等于0；
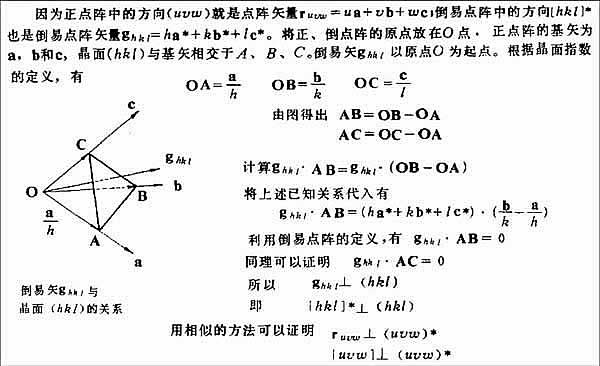
倒易点阵的矢量 r*=ha*+kb*+lc*在方向上与正空间的同名晶面(hkl)垂直，在数值上为正空间点阵中同名晶面(hkl)的面间距的倒数；可以用该倒易点代表与之对应的正空间的晶面；
只有在立方点阵中，晶向才会平行与之同名的晶面的法向；
对于初基点阵来说，正空间属于何种点阵，其相应的倒易点阵也会属于相同的点阵类型；对于非初基点阵来说，底心点阵的倒易点阵仍然是底心点阵，体心点阵的倒易点阵是面心点阵，而面心点阵的倒易点阵则是体心点阵。



4.2 倒易点阵在晶体几何中的应用

倒易点阵的一个重要性质：

倒易点阵的矢量r*=ha*+kb*+lc*在方向上与正空间的同名晶面(hkl)垂直，在数值上为正空间点阵中同名晶面(hkl)的面间距的倒数。





晶带轴定律

设正空间中的某一矢量为：ua+vb+wc；倒空间的任一矢量为： ha*+kb*+lc*；则上面两矢量的点乘为：

当两矢量互相垂直时，其点乘为０，此时有：

给定一个正空间的晶向[uvw]，满足上式的所有晶面(hikili)属于同一个晶带，其晶带轴即为[uvw]；这就是晶带轴定律。

给定一个正空间的晶向[uvw]，对于任一给定的整数N，满足上式的所有晶面(hikili)都在倒空间的同一层倒易面上；该倒易面上的任意矢量(hikili)与晶向[uvw]的点乘都等于整数N，这就是广义晶带轴定律。

倒易点阵的两个重要应用

A、已知两晶面(h1k1l1)、(h2k2l2)，要求这两个晶面所属的晶带轴，只须将与两晶面对应的倒易矢量叉即可，所得的正空间矢量即为两晶面的晶带轴。

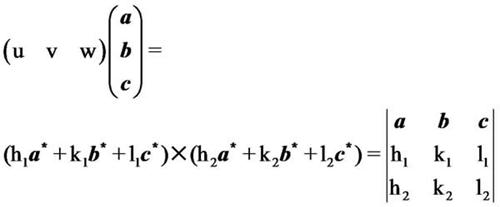
这就是计算电子衍射花样晶带轴的基本公式

B、已知两晶向[u1v1w1]， [u2v2w2]，求其构成的平面(hkl)，只须将两个正空间矢量叉乘即可；


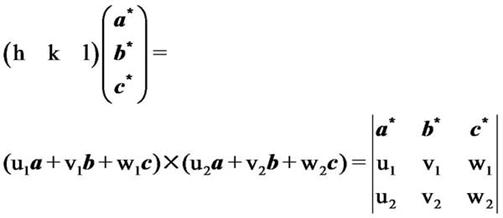
度量张量

由倒易矢量的定义可以知道，倒空间中的三个基矢其实是正空间中与正空间基矢共原点的三个矢量，因此可以用空间变换将两组基矢联系起来，从而将正、倒空间的矢量计算结合起来。

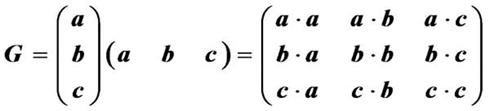
G被称为正空间到倒空间变换的度量张量，它是晶体学计算中一个非常重要的参量。
通过度量张量可以将正倒空间的基矢联系起来：

倒空间的度量张量

同样可以引入倒空间的度量张量G*:

由前面正空间基矢与倒空间基矢之间关系式可以求出正倒空间之间度量张量之间的关系，同时也可以求出倒空间基矢用正空间基矢表示时的表达式。下面是推导过程：

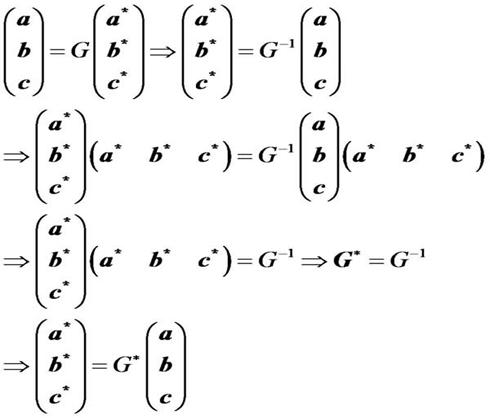
正、倒空间基矢的计算

对于任意给定的已知晶体，其正空间的晶格常数应该是已知的，由前面推导出来的公式，我们同样可以求出倒空间的晶格常数。

正空间的度量张量用基矢表示可以写为：

求其矩阵的逆矩阵可以得到：


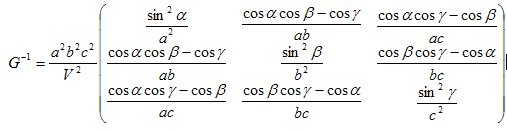
倒空间的度量张量的表达式为：

因为倒空间的度量张量与正空间的逆矩阵是相等的，所以上面两个表达式中每一项都应该是对应相等产的。据此可以马上得到倒空间的晶格常数用正空间晶格常数来表示的表达式：


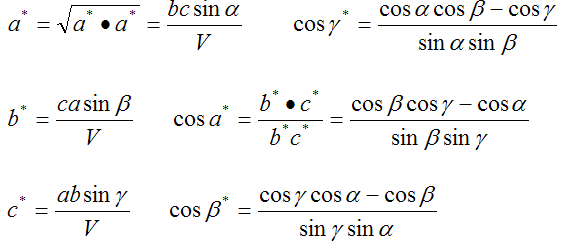
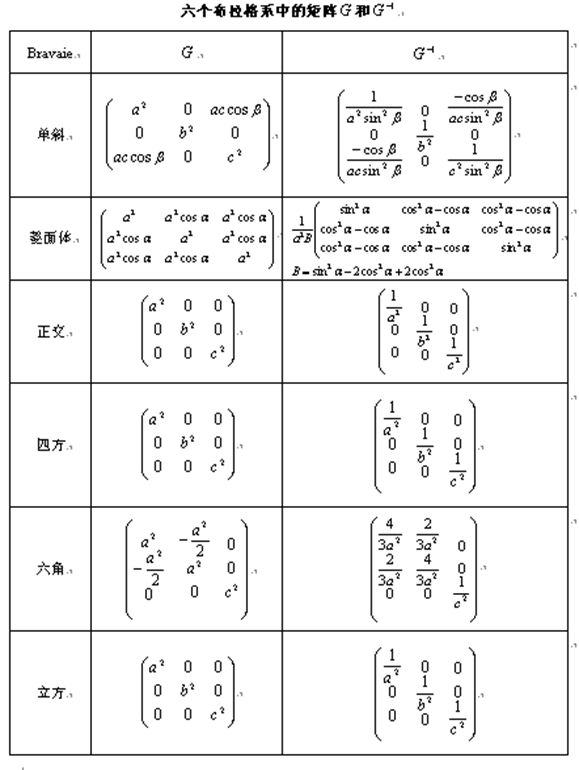
在晶体学计算时，经常要用到正空间和倒空间的度量张量，下面是六大晶系度量张量的表达式（三斜晶系在前面已经给出）

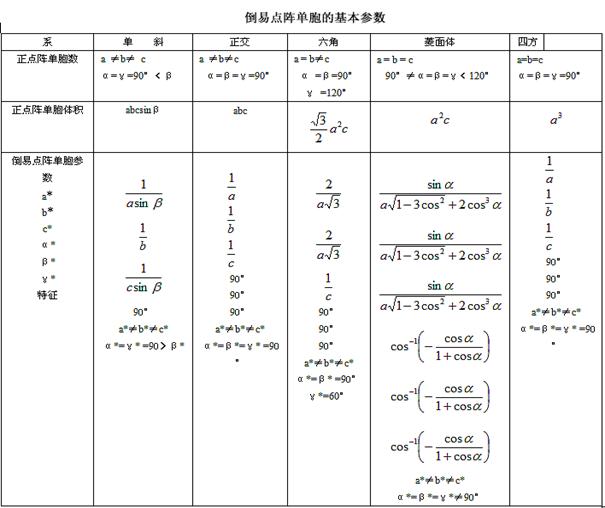
由上面这些矩阵，用类似于求三斜晶系倒空间晶格常数的办法，可以求出其它所有晶系的晶格常数的表达式，下表即是各大晶系倒易点阵单胞的基本参数表：

由上表我们可以得出一个非常重要的结论：

对于同一种晶体，其正空间是属于何种晶系，那么其倒空间同样也是属于该种晶系。

利用度量张量的概念，可以非常方便地求出晶体中的晶面间距、晶面之间的夹角、晶向长度和晶向之间的夹角。

各晶系的晶面间距、晶面之间的夹角、晶向长度和晶向之间的夹角如下表所示：